SICP and Expression Problem (下)
expression problem
密涅瓦的猫头鹰,只有在黄昏的时候才起飞 –黑格尔
导读
本文是我个人的读书笔记,很多地方引用原文。
读了很多资料,写的一个个汇总。笔记和阅读的资料相关,不成体系的,如果真要找一条线,那就是希望找到技术问题共同的本质难点,这样难免会与数学的关联。
expression problem作为引子,用函数式编程语言OCaml和面向对象语言Java,分别解决这个问题。这其实应该是本文的思考起点和中心的,整片文章就是思考这个问题,并回忆所读的书籍写出来的。只是没想到牵扯了这么东西,这导致本文的叙述很乱,没有一个清晰的结构。
简要介绍一下OCaml的变体(variant)和多态变体(polymorphic variant),了解一下sum类型的使用。介绍Sum类型时附带介绍Java的异常声明(Checked Exception)。并用OCaml解决expression problem。
利用访问者模式(visitor pattern)处理此问题,并进一步用Object Algebras处理expression problem。
后续转入介绍一下 Algebraic data types,只能作为朴素的理解,不成系统。
简单介绍了代数类型里面的Product类型和Sum类型(union类型),以及其和代数之间的同构。
接着介绍Lisp中列表的类型和二叉树的类型,然后是Zipper与求导的关系,二叉树的挖洞。
以及与此关系很弱的Git的底层的数据结构设计。为什么要加Git的设计呢?
所引用的书,文中涉及的部分,都是阅读过,并且自己写代码,OCaml的代码是读了《The Real World OCaml》,自己想出来的,估计不是最佳方案。但很长一段时间,被一篇用OCaml解决expression problem的实现误导了,思考了很久,算是一种别样的阅读体验。好多年没写Java,这是头一次,代码也自己参考技术博客,然后自己修改的,保证可以运行,但代码风格不能保证。搜索访问者模式的资料,发现各个资料的实现,各有不同,加上我对Java不熟悉,这里的实现存疑。请教了几位同事,当前实现应该没有硬伤。
Java代码和OCaml代码,并不是一一对应。本想改成一一对应的,后来想一下,其实不影响主题的诠释,就懒得修改了。
完整可运行代码见code of SICP and Expression Problem。所有的代码均保证可以运行。
expression problem
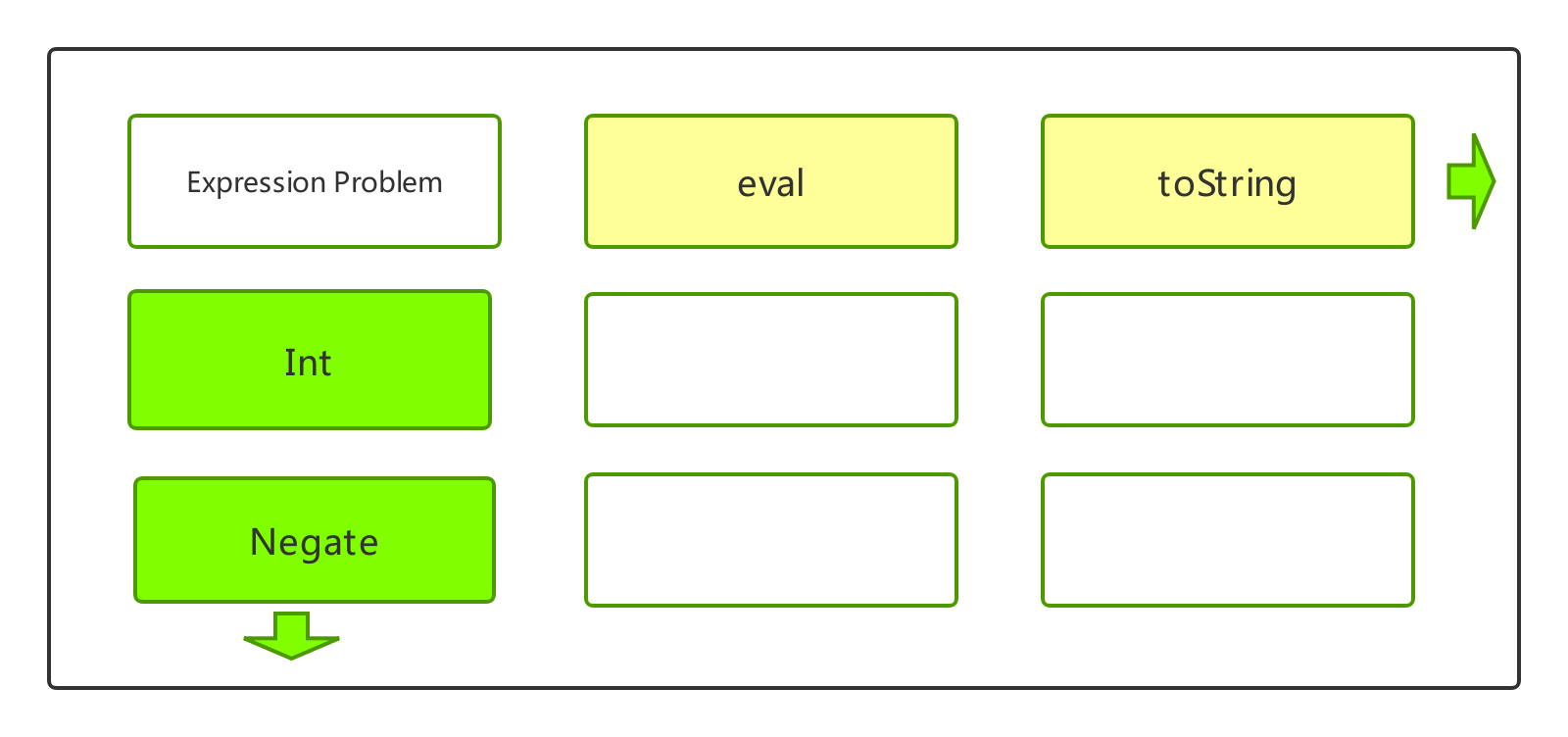
数据类型和函数是程序的两个维度,他们之间存在映射关系。数据可以应用在多个算法上,函数也可以操作多个数据。但我们的代码是维度只有一个,按顺序从上到下写。以数据为主来组织代码,如:面向对象;以函数来组织代码,如:函数式编程。
当程序需要在两个维度——数据和函数——都需要拓展的时候,两者有各自不同的优势和劣势。在类型安全的前提下,新增数据类型,并新增对应的函数的问题,即expression problem。
The Expression Problem is a new name for an old problem. The goal is to define a datatype by cases, where one can add new cases to the datatype and new functions over the datatype, without recompiling existing code, and while retaining static type safety (e.g., no casts). For the concrete example, we take expressions as the data type, begin with one case (constants) and one function (evaluators), then add one more construct (plus) and one more function (conversion to a string). – Philip Wadler
OCaml解决expression problem
前置知识
variant
联合类型(sum)也称变体(variants)。
联合类型来源于集合论中的不相交并集(disjoint union)。这个概念不同于并集(union)。
两个集合A和B的并集是:A∪B={x|x∈A∨x∈B}
不相交并集是指两个集合中所有的元素都合并到一个集合中,并且每一个集合的元素都带有原集合的标记。可以表示为:
A + B={(a, 0)|a∈A} ∪ {(b, 1)|b∈B}
其中,0是A的标记,1是B的标记。0和1可以用任意符号代替。在OCaml中,不相交并集的每一个集合,该集合的特征的标识符来做这个集合的标记,这个标记用于构造联合类型中的一个元素,因此也称为联合类型的构造子(constructor)。“构造子”通常指用于构造某种语言成分的标识符。
构造子可以分为两类,一类带参数,另一类不带参数。后者称之为常量构造子,如:拥有常量构造子的联合类型相当于枚举类型,本身就是数据或者值。
以上引用自陈钢的《OCaml语言编程与基础教程》
sum类型用伪码表示: def type T = A | B
类型T实例化之后,可能是A类型或者B类型。类似于多态。
可以类比C/C++的enum structure,不过,enum枚举的是变量。
sum 类型(union 类型)和Java的异常声明(Checked Exception)
Java的异常设计和C++类似,C++异常借鉴了CLU。从中带来了一个思想:异常声明。即,用编程的方式在方法特征签名中,声明这个方法将要抛出的异常。异常声明意味着:
- 我的代码产生这种类型的异常,由你来处理;
- 我的代码忽略这些异常,这由你来处理。
这两句口语,道出了异常的一个重要目标:错误处理的代码同错误发生地点相分离。通过这中方式来规避业务代码与处理错误的代码混淆的麻烦。降低了处理错误的代码的复杂度,容易理解和维护。
Java的异常声明,能在编译阶段保证异常的正确性。
函数的类型里声明可能抛出的异常:
String fun() throw MyException {
// ...
if (/* ...*/) {
throw new MyException();
}
}
Java要求必须在函数头部写上throws MyException,否则不能编译。这个声明表示函数fun可能会抛出 MyException 异常。编译阶段看到这个声明,就会严格检查fun的用法,调用这个函数的时候,需要处理对应的异常。如:
try {
fun();
} catch (MyException e) {
// ...
}
我们可以把函数的返回值和异常一起,看作一个“sum类型”。
fun的返回类型,可以看作:(String, MyException)。调用fun的代码,必须合理处理 MyException。Java要求函数需要声明可能的异常,而且强制调用者需要处理这些异常。这样就有一个比较严格的异常处理,避免遗漏。
异常throw与函数返回值类似,函数调用throw异常了,从调用函数的角度看,函数此时也返回了,可以简单的把异常看作一种不同的返回机制。
然而,异常与返回值还有不同的地方。异常将在异常处理程序中得到解决,异常处理程序可能离异常非常远,甚至可能跨越方法调用栈很多层。这和普通方法的返回完全不同。
异常检查使得异常处理有了约束,有人为了摆脱这种约束,写了吞食有害的代码(harmful if swallowed,来自《Java编程思想》)
try {
fun();
} catch (ObligatoryException e) {} // Gulp!
这种做法很省事,但会付出代价。就像生病了,拒绝吃药治疗,迟早病入膏肓。
catch异常的时候,要catch正好可能发生的异常,不是使用非常宽泛的异常,因为这样可能会catch意料之外的异常。
同时,最好在恰当的时候处理异常,不要简单的把下层异常加到自己的函数里,然后抛出。这样,多层调用之后,会导致后面的函数积累了非常多的异常,调用者难以处理,最好直接抛出宽泛的异常throw Exception。
Java要求对异常进行显示声明,实质上就是把一个需要全局分析的问题,分解成一个个模块化的小问题。函数的作者完成一部分,调用中完成一部分,编译进行异常检查,防止遗漏的异常,避免不必要的try-catch。(JavaScript中就只有类似于全局的try-catch)
来自《Java编程思想》 Thinking in Java (Fourth Editron) by Bruce Eckel
Checked Exception类似于 union type的思想,来自于王垠。《编程的智慧》和《Kotlin 和 Checked Exception》提及这一思想。原文写得非常,这里我自己并没有深刻见解,原文直接引用。
模式匹配
function
| 类型1 -> 代码1
| 类型2 -> 代码2
... ...
)
变体(variant)实现expression
(*定义表达式的类型:Int Negate Add*)
type exp =
Int of int
| Negate of exp
| Add of exp * exp
(*实现求值*)
let rec eval = function
| Int i -> i
| Negate e -> -(eval e)
| Add(e1, e2) -> (eval e1 ) + (eval e2)
(*实现把表达式转化为字符串*)
let rec toString = function
| Int i -> string_of_int i
| Negate e -> "-(" ^ (toString e) ^ ")"
| Add(e1, e2) -> "(" ^ (toString e1) ^ "+" ^ (toString e2) ^ ")"
;;
(*测试代码*)
let res = toString (Add ((Negate (Int 5)), (Int 6)));;
let num = eval (Add ((Negate (Int 5)), (Int 6)));;
从类型-操作表格角度分析
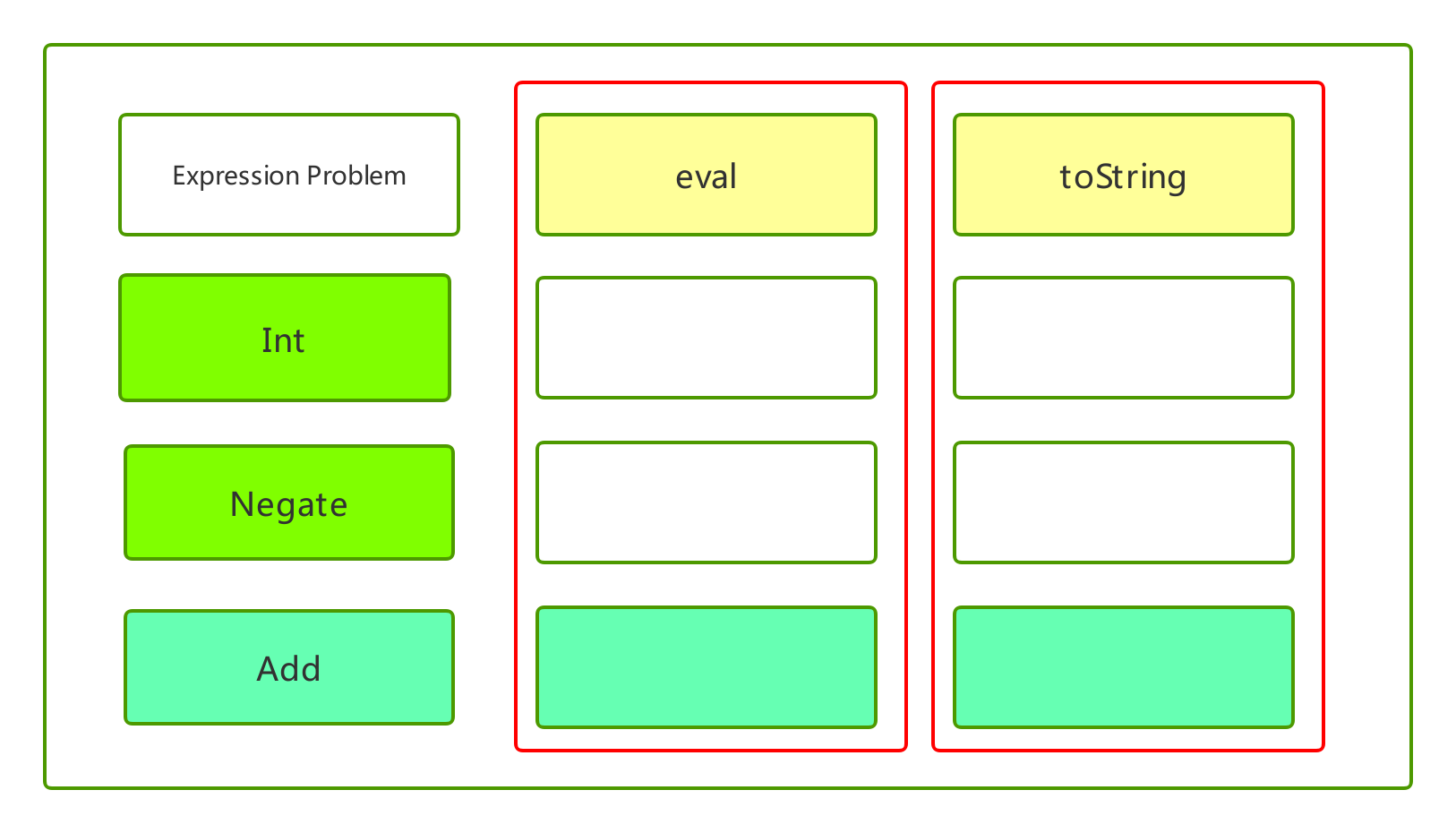
variant实现的expression,表达式的类型是固定的,无法拓展。但操作可以随意添加,我们还可以添加其他操作,模式匹配保证了类型安全。如果操作支持的类型不全,模式匹配就会报错。
我们实现toString的时候,忘记实现Add的,模式匹配就会报错:
缺失Add实现toString的代码:
let rec toString = function
| Int i -> string_of_int i
| Negate e -> "-(" ^ (toString e) ^ ")"
编译时的报错:
File "exp.ml", line 11, characters 19-98:
11 | ...................function
12 | | Int i -> string_of_int i
13 | | Negate e -> "-(" ^ (toString e) ^ ")"
Warning 8: this pattern-matching is not exhaustive.
Here is an example of a case that is not matched:
多态变体(polymorphic variant)
常规变体需要先定义,再使用,且在其他变体中不能使用。多态变体,可以直接使用,且多个多态变体可以共享构造子名字,使得我们可以在多态变体类型的基础上拓展。这与OCaml对子类型(subtyping)的支持紧密相关。子类型会带来大量的复杂性。
如果一个类A中的方法都包含在另一个类B中,则A和B之间具有子类型关系。子类(subtyping)关系是子类型关系的一种特殊情况。subtyping是面向对象编程中的一个核心概念。决定了C类型的对象什么时候可以用在原本需要D类型对象的表达式中。
多态变体缺点:
- 复杂性
- 错误查找。多态变体是类型安全的,不过由于其灵活性,他的类型约束不太可能捕获程序中的bug
- 效率。OCaml为匹配多态变体时,无法向常规变体那样生成同样高效的代码
以上引用自《Real World OCaml》。
多态变体(polymorphic variant)解决expression problem
使用多态变体实现exprssion,使得variant具有拓展能力。
type exp =
[`Int of int
| `Negate of exp
| `Add of exp * exp]
let rec eval = function
| `Int i -> i
| `Negate e -> -(eval e)
| `Add(e1, e2) -> (eval e1 ) + (eval e2)
let rec toString = function
| `Int i -> string_of_int i
| `Negate e -> "-(" ^ (toString e) ^ ")"
| `Add(e1, e2) -> "(" ^ (toString e1) ^ "+" ^ (toString e2) ^ ")"
多态变体的缺点
但也失去模式匹配和类型推导的好处,无法检测是否覆盖所有类型。
我们实现toString的时候,忘记实现Add的,模式匹配不再报错,可以直接通过编译。
缺少Add的toString实现:
let rec toString = function
| `Int i -> string_of_int i
| `Negate e -> "-(" ^ (toString e) ^ ")"
这时,需要手动写明函数的类型,如
let rec toString : exp -> string = function
| `Int i -> string_of_int i
| `Negate e -> "-(" ^ (toString e) ^ ")"
| `Add(e1, e2) -> "(" ^ (toString e1) ^ "+" ^ (toString e2) ^ ")"
此时,如果我们忘记实现Add的,就会报错:
File "exp_exhaustive.ml", line 13, characters 35-116:
13 | ...................................function
14 | | `Int i -> string_of_int i
15 | | `Negate e -> "-(" ^ (toString e) ^ ")"
Warning 8: this pattern-matching is not exhaustive.
Here is an example of a case that is not matched:
`Add _
多态变体的优点
多态变体就有可拓展性,可以用多态变体解决expression problem。
我们新增一种表达式。
type new_exp = [ exp | `Sub of new_exp * new_exp]
支持eval求值操作和toString操作:
let rec new_eval : new_exp -> int = function
| #exp as exp -> eval exp
| `Sub(e1, e2) -> (new_eval e1) - (new_eval e2)
let rec new_toString : new_exp -> string = function
| `Sub(e1, e2) -> "(" ^ (new_toString e1) ^ "-" ^ (new_toString e2) ^ ")"
| #exp as exp -> toString exp
expression的实现,其实一个初步interpreter,附录有一个相对完整的用Racket实现的interpreter。本想用OCaml实现一遍,Lisp看起来差不多,没必要。Racket还有一个好工具DrRacket,OCaml我暂时只有utop可用,虽然很方便,但不如DrRacket,后者具有IDE的功能。
Java解决expression problem
visitor,本质上是函数式编程语言里的含有“模式匹配pattern matching”的递归函数。 – 王垠
从类型-操作表格分析
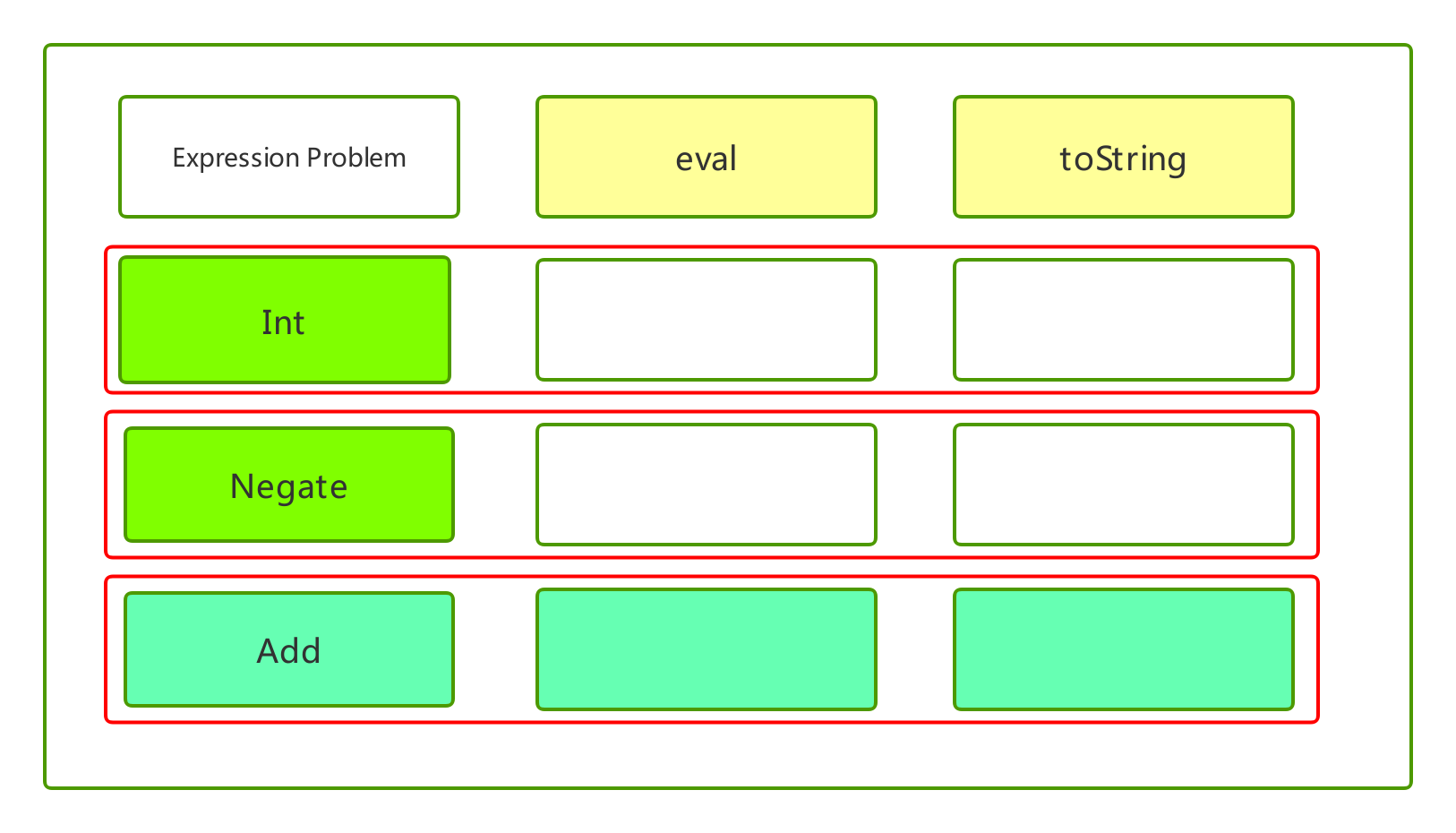
我们用Java来解决expression problem。在Java中,expression用Class来声明。与函数式编程语言相反,Java中很方便新增expression,新增Class即可。但新增操作就很不方便,需要去修改每一个表达式的Class,逐一加上新操作。
解决这个拓展问题的办法是访问者模式(Visitor Pattern)。这个模式很厉害,是Friedman的《A Little Java, A Few Patterns》中讲解的模式。Friedman的Little系列的书,很厉害,如《The Little Typer》,讲dependently typed,如《The Little Schemer》,讲递归和Scheme。当然,系列书风格一致,类似于古希腊的柏拉图的《理想国》,很话痨,但很细致深刻。
Visitor Pattern
我们把操作抽象出去,集合在Class中,然后把这个Class,用参数传递各个expression的方法里。
interface Exp {
<T> T accept(ExpVisitor<T> visitor);
}
interface ExpVisitor<T> {
public T forLiteral(int v);
public T forAdd(Exp a, Exp b);
}
// 定义expression
class Literal implements Exp {
public final int val;
public Literal(int val) {
this.val = val;
}
public <T> T accept(ExpVisitor<T> visitor) {
return visitor.forLiteral(val);
}
}
// eval求值操作
class ExpEvalVisitor implements ExpVisitor<Integer> {
@Override
public Integer forLiteral(int v) {
return v;
}
@Override
public Integer forAdd(Exp a, Exp b) {
return a.accept(this) + b.accept(this);
}
}
显然在访问者者模式中,新增操作非常容易,直接implements ExpVisitor即可。
新增操作
// 返回对应的字符串的操作
class ExpShowVisitor implements ExpVisitor<String> {
@Override
public String forLiteral(int v) {
return v + "";
}
@Override
public String forAdd(Exp a, Exp b) {
return "(" + a.accept(this) + "+" + b.accept(this) + ")";
}
}
新增类型
我们拓展一下这个实现,新增一种操作:除法Divide。
// 拓展接口
interface ExpVisitor2<T> extends ExpVisitor<T> {
public T forDivide(Exp a, Exp b);
}
interface Exp2 {
public abstract <T> T accept(ExpVisitor2<T> visitor);
}
// 继承ExpEvalVisitor,拓展ExpEvalVisitor
class ExpEvalVisitor2 extends ExpEvalVisitor implements ExpVisitor2<Integer> {
@Override
public Integer forDivide(Exp a, Exp b) {
return a.accept(this) / b.accept(this);
}
}
// 实现新的expression,除法
class Divide implements Exp2 {
public final Exp a;
public final Exp b;
public Divide(Exp a, Exp b) {
this.a = a;
this.b = b;
}
public <T> T accept(ExpVisitor2<T> visitor) {
return visitor.forDivide(a, b);
}
}
Object Algebras
在访问者者模式中,expression的实现,还可以进一步简化抽象。
interface Exp<T> {
public T literal(int v);
public T add(T a, T b);
}
class Eval implements Exp<Integer> {
@Override
public Integer literal(int v) {
return v;
}
@Override
public Integer add(Integer a, Integer b) {
return a + b;
}
}
新增方法
class Show implements Exp<String> {
@Override
public String literal(int v) {
return v + "";
}
@Override
public String add(String a, String b) {
return "(" + a + "+" + b + ")";
}
}
新增类型
interface Exp2<T> extends Exp<T> {
public T divide(T a, T b);
}
class Eval2 extends Eval implements Exp2<Integer> {
@Override
public Integer divide(Integer a, Integer b) {
return a / b;
}
}
Object Algebras总结
以上实现,被称之为Object Algebras。
- Data type is generic factory interface
- Operation is factory implementation
- Easy to add variants(extend interface)
- Easy to add operations(implement interface)
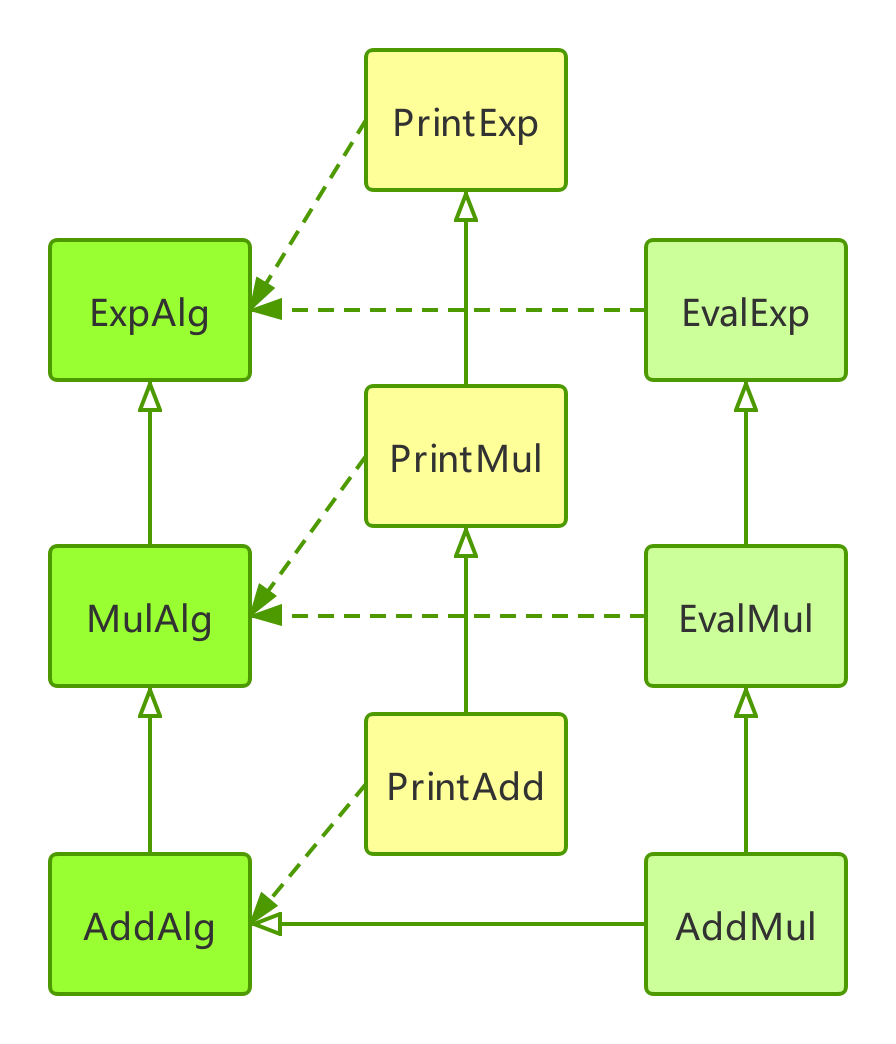
通过extend和implement拓展原来的代码,Class之间有清晰的层次关系,我们可以类比Algebraic data types,这一系列的Class结构,和代数之间,也可以构造一个可逆映射(同构)。
代数数据类型(Algebraic data types)
代数数据类型与代数
代数数据类型(Algebraic data types),是一种组合类型,“代数”一词是因为有两种代数类型,主要是 Product 类型(如元组和记录,在代数上类似于笛卡尔乘)和 Sum 类型(如变体,在代数上类似于 Disjoint Unions,即交集为空集的集合的并操作)。代数类型在模式匹配中极为重要的。
正如其名,代数数据类型代表相应的数据结构应该满足一定的数学属性,利用相应的关系,我们可以用来证明类型实现的正确定,进一步证明程序的正确性。另一方法,它鼓励合理利用composition去构建更复杂的数据结构和算法。
OCaml有两种类型:记录类型(records)和联合类型(sums)。记录类型和C语言中的结构体(struct)类似,联合类型与C语言的(union)可以类比,但内容更为丰富。
C语言从存储分配角度解释结构体和联合体,OCaml则是从数学基础和语义角度解释记录类型和联合类型。记录类型是集合论中的笛卡尔积的推广,而联合类型则是不相交集合(disjion union)的推广。联合类型可用于构造枚举类型,也可以用于构造递归数据结构。表结构是递归数据结构的特例。
C语言的结构体和联合体内的分量是可以修改的,但OCaml的记录和联合体的分量,都是不可以修改的。内部结构不可以修改的数据类型称为函数式数据类型(funcitonal data structure)
以上引用自陈钢的《OCaml语言编程与基础教程》
类型(数据结构)和代数之间构造一个可逆映射(同构), 这就是为什么称为代数数据类型, 可以采用代数方式对类型进行运算。
类型可以定义为所有可接受值的集合
空类型(Void): 不接受任何值, 映射至自然数0
单位类型(Unit): 只接受一种可能值, 映射至自然数1
在类型上定义加法与乘法
-
加法:
a + b = {x or y | x ∈ a, y ∈ b} -
乘法:
a * b = { (x , y) | x ∈ a, y ∈ b}(笛卡尔乘积)
可以证明类型上的加法与乘法具有代数加法与乘法相同性质(交换律, 结合律, 分配律)。并且空类型为加法单位元, 单位类型为乘法单位元。
具体来说:
- 普通类型对应代数变量
- 数据构造器或 Tuple 对应求积
|操作符对于求和
即:
Int <==> int
MyType Int Int or (Int,Int) <==> int*int
Left Int | Right Int <==> int+int
用这个关系,我们反推一下列表[a]的类型,列表要么是0个元素,1个元素,或者2个元素,如整数一样,以此类推….:
1 + a + a * a + a * a *a + ...
= 1 + a( 1 + a + a * a + ....)
可以看出,列表类型有不动点f(x)=1 + a * x或者循环不变式1 + a * x。
即列表有:
List(TypeX) = Unit + TypeX * List(TypeX)
得到:
L(x) = 1 + x * L(x)
解出可得:
L(x) = 1 / (1 - x)
考虑二叉树的类型:
Tree(TypeX) = Unit + Unit * Tree(TypeX) ^ 2
一颗树可以为空树, 包含0个节点, 为Unit, 或者一个元素(树根)下为左子树与右子树. 这个为二叉树的递归定义. 对应的代数形式:
T(x) = 1 + x * T(x) ^ 2
解方程,得到T(x)为:
T(x) = (1 - (1 - 4 * x))/(2 *x)
进行泰勒展开得到:
T(x) = 1 + x + 2 * x ^ 2 + 5 * x ^ 3
其中x ^ n(x的n次方)对应于总节点数为n的二叉树,系数表示所有可能树的结构数目:

二叉树(binary tree)
二叉树的类型定义
陈钢的《OCaml语言编程与基础教程》(2018.6版本)第70页,定义的二叉树类型是错误的,缺失节点的元素。
- 错误的二叉树定义
type inttree = Leaf of int | Node of inttree * intree
- 错误的用多态变量定义的二叉树
type 'a tree =
| Leaf
| Node of 'a tree * 'a tree
- binary tree
type 'a tree =
| Leaf
| Node of 'a * 'a tree * 'a tree
- list
type 'a mylist =
| Nil
| Cons of 'a * 'a mylist
二叉树和list的类型定义,使用联合类型(sums)构造的递归数据类型。我们可以看到,二叉树和表都是递归数据结构。
构造一个简单的二叉树
(* the code below constructs this tree:
4
/ \
2 5
/ \ / \
1 3 6 7
*)
let t =
Node(4,
Node(2,
Node(1,Leaf,Leaf),
Node(3,Leaf,Leaf)
),
Node(5,
Node(6,Leaf,Leaf),
Node(7,Leaf,Leaf)
)
)
求二叉树的深度
let rec size = function
| Leaf -> 0
| Node (_, l, r) -> 1 + size l + size r
Zipper与求导
函数式程序设计中,不允许修改数据,只能创建新的数据达成修改的目的。当数据很大的情况下,复制原来的数据,并修改之,得到新数据,成本很高。还有一个办法,就是只修改需要修改的局部即可,复用旧数据创建新数据。避免了deepCopy复制带来的消耗。
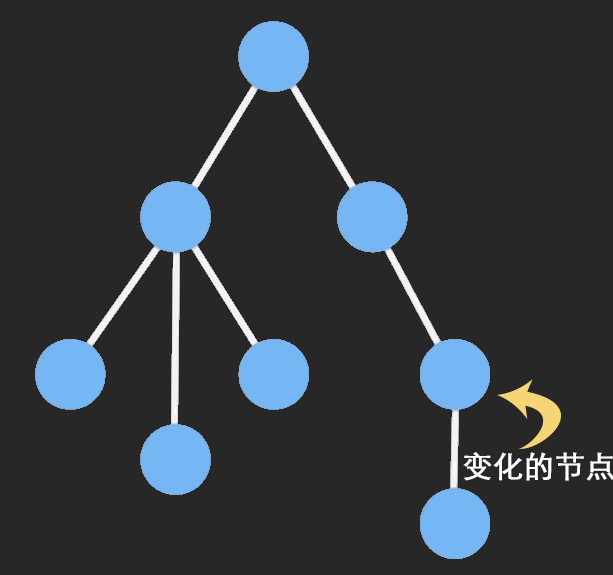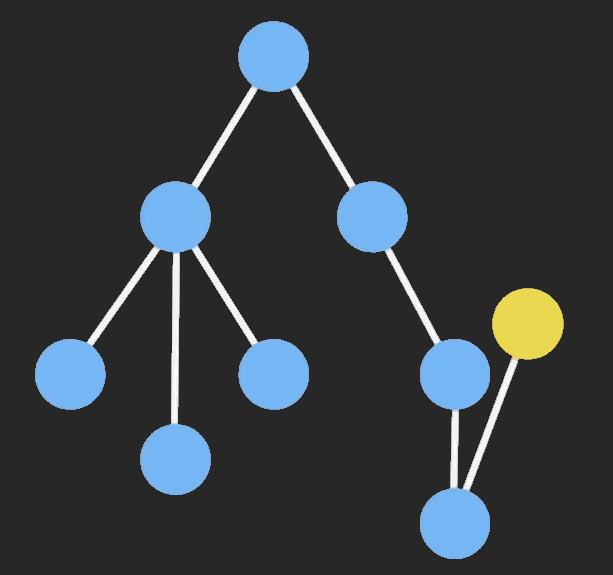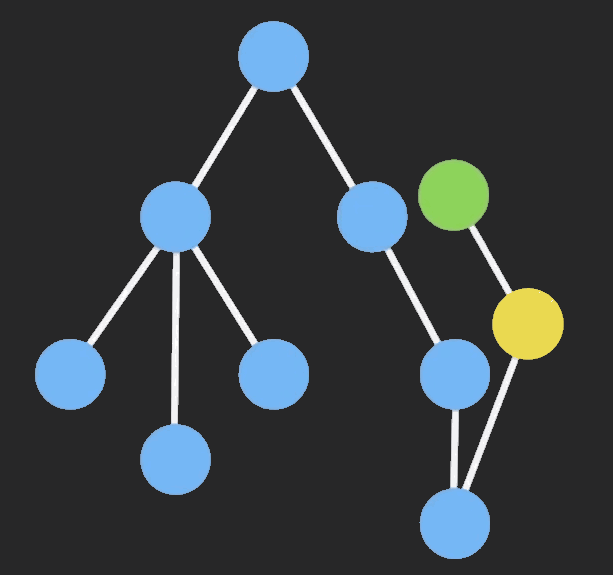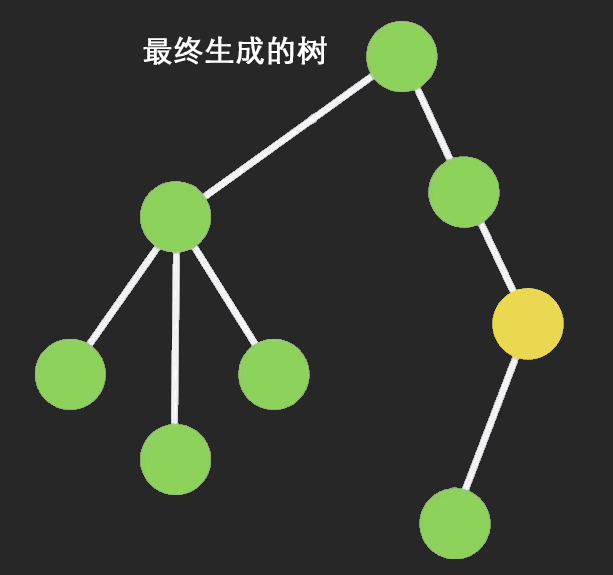
要达到这个目的,需要知道类型的局部特征。
求导产生了一个新的类型, 这个类型正好是原类型中从中挖去一个元素留下一个洞(Unit)的类型(One-Hole Contexts)。 这种类型在函数式编程语言里非常有用, 对该类型乘元素类型补全, 将得到与原类型结构相同并同时拥有局部性的类型。
举个例子,包含三个整数的积类型: int*int*int ,或者 int ^ 3的三次方,用tuple的表示法就是 (Int, Int, Int) ,要挖个洞的话有三种挖法:
(_, int, int)
(int, _, int)
(int, int, _)
即int*int + int*int + int*int,加起来之后,即3 * int * int,即3 * int ^ 2。正好是a ^ 3求导的结果3 * a ^ 2。
对于二叉树有:挖去元素后列表断开, 剩下以该节点为树根的左右子树和从树根到该节点的路径上的每一个节点与其非路径节点的子树构成的列表, 路径上的每一个节点的非路径节点子树有两种可能(左或右子树)。
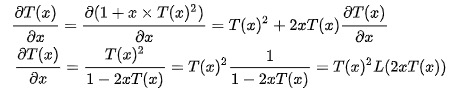
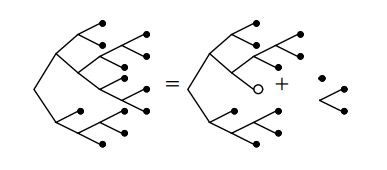
即为:
T(x)^2*L(2xT(x))T(x)^2为该节点下的左右子树。
L(2xT(x))为一个列表, 记录从树根到该节点的路径, 列表里的每一个元素类型为2xT(x)2xT(x), x为路径上的一个节点, T(x)为该节点相连的非路径节点的子树, 2表示该非路径节点的子树应为左子树或右子树.
对于一个代数式进行求导有明确的分析意义. 但对于一个类型进行求导的直观意义就非常微妙了, 得到的是带有洞的新类型. 这之间的联系也许是”巧合”, 也许揭示了类型与分析之间存在更为深刻的关联.
Git与不可变数据
SVN与Git的diff的不同
大多数系统(比如CVS和SVN)会跟踪一系列修订版本,并只存储文件间的差异。这个策略是为了节省空间和开销。
在Git中,如你所见,每一个提交都包含一棵树,也就是该提交包含的文件列表。每一个树都是跟其他书独立的。Git的用户也会谈论diff和patch,当然,因为这些依旧相当有用。但是,在Git中,diff和patch是导出的数据,而不是SVN或者CVS中的基本数据。
每个修订版本有一颗自己的树,但Git不需要他们来生成diff;Git可以直接操作两个版本的完整状态的快照。存储系统中这个简单的差异是Git比其他RCS速度快得多的最重要原因之一。
SVN之类的系统中,需要很多时间去思考这样的问题:“在A文件和B文件之间有什么差异”。如:当你从中心版本库更新文件的时候,SVN会记着你上次更新时是版本r1095,但这次更新时版本已经到了版本r1123。因此,服务器必须把r1095和r1123之间的diff发给你。一旦你的SVN客户端有了这些diff,他就可以把这些diff合并到你的工作副本中,从而产生r1123。这样就避免了,每次更新的时候发送所有文件的全部内容。
Git可以检索和生成任意两个版本之间的差异。但这个过程中,SVN要查看版本r1095和版本r1123间的所有版本,而Git则不关心这些中间步骤。
Git追踪内容(content tracking system)
Git不仅仅是一个VCS,还是一个内容追踪系统(content tracking system)。Git的内容追踪主要表现为两种关键方式,与其他多数版本控制系统不一样。
首先,Git的对象库,基于对象内容的散列计算的值。而不是基于用户原始文件的文件名或目录。Git追踪的是文件内容,而不是文件名或者目录。如果文件对应的blob有相同的SHA1值,则内容相同,无论文件在用户什么目录,都只有一个blob对象。如果,文件发生了变化,Git会计算一个新的SHA1值,标识新的blob对象。
其次,文件从一个版本到另一个版本,Git内部的数据会存储文件的每一个版本,而不是他们的差异。因为Git使用一个文件的全部内容的SHA1散列值,所以必须针对每一个文件的完整副本。Git不能把SHA1散列值建立在文件内容的一部分或者文件的两个版本之间的差异上。
这样可能导致的问题:
直接存储每一个文件每一个版本的完整内容的效率是否太低了?如果只修改了一行到文件里,是不是存储两个版本的全部内容?
答案是“不是,不完全是!”
Git使用一种叫做打包文件(pack file)的存储机制。Git是内容驱动的,并不真正关心计算出来的两个文件之间的差异是否属于同一个文件的两个版本。Git还维护打包文件表示中每个完整文件(包含完整内容的文件和通过差异重建出来的文件)的原始blob的SHA1值。这个给定位包内对象的索引机制提供了基础。
Git创建一个打包文件,首先会定位内容非常相似的全部文件,然后为他们之一存储整个内容。之后计算相似文件之间的差异并且只存储差异。
如果只修改了一行。Git可能会存储新版本的全部内容,然后记录那一行更改作为差异,并存储在包里。(感觉作者叙述不清晰,并没有说明Git与存储diff的版本管理的区别)
在原文的基础上略有修改,以方便诠释主题。
–《Version Contorl with Git》 by Jon Loeliger and Matthew McCullough
循环不变式
命题=类型(Propositions as Types),程序=证明。
我认为程序员可以被分为两种:
- 先确认前条件/不变式/终止条件/边界条件,然后写出正确的代码
- 先编写代码,然后通过各种用例/测试/调试对程序进行调整,最后得到似乎正确的代码 我个人保守估计前者开发效率至少是后者的 10 倍,因为前者不需要浪费大量时间在编码-调试-编码,这个极其耗时的循环上。
《算法导论》(Introduction to Algorithms)的第二章“算法基础”,2.1节插入排序“循环不变式与插入排序的正确性”。
循环不变式主要用来帮助理解算法的正确性。形式上很类似与数学归纳法,它是一个需要保证正确断言。对于循环不变式,必须证明它的三个性质:
《算法导论》中的循环不变式的概念与性质:
初始化:循环的第一轮迭代开始之前,为真
保持:如果在循环的某一次迭代开始之前为真,那么在下一次迭代开始之前仍为真
终止:在循环终止时,不变式为我们提供一个有用的性质,该性质有助于证明算法是正确的
类似于数学归纳法,其中为了证明某条性质成立,需要证明一个基本情况和一个归纳步。
第三条性质也行最重要,因为我们将使用循环不变式来证明正确性。通常,我们和导致循环终止的条件一起使用循环不变式。终止性不同于我们通常使用数学归纳法的做法,在归纳法中,归纳步是无限使用的,这里当循环终止时,停止“归纳”。
分析插入排序:
//将arr[i] 插入到arr[0]...arr[i - 1]中
public static void insertion_sort(int[] arr) {
for (int i = 1; i < arr.length; i++ ) {
int temp = arr[i];
int j = i - 1;
//如果将赋值放到下一行的for循环内, 会导致在第10行出现j未声明的错误
for (;j >= 0 && arr[j] > temp; j-- ) {
arr[j + 1] = arr[j];
}
arr[j + 1] = temp;
}
}
下标j指出需要排序的元素,而arr[0...j-1]已经排序了。把arr[i]插入其中即可。在迭代中这个性质保持不变,我们把A[0...j-1]的这些性质,形式的表示为循环不变式。
- 初始化:当
j = 0,1,2时显然成立 - 保持:内部for循环,把索引小于j的元素,右移一位,直到找到
arr[j]的适当位置,然后插入此位置。此时,子数组arr[0...j],已按照顺序排列。保持了循环不变式。 - 终止:当i大于
arr.length时,终止。即j = arr.length。此时,j = arr.length,有:子数组arr[0..arr.lenght]已经按顺序排列。即,整个数组已排序。因此,算法正确。
反思
误导的技术文章
Mu Xian Ming的OOP vs FP:用 Visitor 模式克服 OOP 的局限》中错误的OCaml实现:
exception BadResult of string
type exp =
Int of int
| Negate of exp
| Add of exp * exp
let rec eval e =
match e with
Int _ -> e
| Negate e1 -> (match eval e1 with
Int i -> Int (-i)
| _ -> raise (BadResult "non-int in negation"))
| Add(e1,e2) -> (match (eval e1, eval e2) with
(Int i, Int j) -> Int (i+j)
| _ -> raise (BadResult "non-ints in addition"))
let rec toString = function
Int i -> string_of_int i
| Negate e1 -> "-(" ^ (toString e1) ^ ")"
| Add(e1,e2) -> "(" ^ (toString e1) ^ " + " ^ (toString e2) ^ ")"
let rec hasZero = function
Int i -> i = 0
| Negate e1 -> hasZero e1
| Add(e1,e2) -> (hasZero e1) || (hasZero e2)
;;
toString (eval (Add ((Negate (Int 5)), (Int 6))))
(* - : string = "1" *)
以上代码用于举例说明,在expression problem这个场景中,函数式程序设计,易于增加方法,不易于增加类型。后面有一到两个星期,我都在思考,怎么拓展这段代码,用OCaml解决expression problem。
而作者给出的解决方案,看起来似乎可行,可是实际上是错上加错。
对于函数式模式来说,可以在类型定义中增加一个“其他”的类型,然后所有的函数都接受一个额外的函数类型的参数来处理“其他”的数据类型。
type ’a ext_exp =
Int of int
| Negate of ’a ext_exp
| Add of ’a ext_exp * ’a ext_exp
| OtherExtExp of ’a
let rec eval_ext (f, e) =
match e with
Int i -> i
| Negate e1 -> 0 - (eval_ext (f, e1))
| Add (e1, e2) -> (eval_ext (f, e1)) + (eval_ext (f, e2))
| OtherExtExp e -> f e
第一次看到这段代码,以为用这种额外通用的办法是可以的。由于我函数式编程语言中,实际能编程的只有Scheme和OCaml,很多文章讲解expression problem都是用Haskell,而Haskell的处理是其语言的思路,根本不能借鉴到OCaml中。
于是研究这个篇文章中的代码,花了很多时间,改模式匹配的代码,越改越复杂,生成非常复杂的类型错误。后面阅读到cornell CS 3110课程PPT,才恍然大悟,这个博客里最初的代码就是错误的,模式匹配根本就不对,而作者为了掩盖模式匹配错误,给每一个函数都加上了_匹配,然后扔掉,导致也不会报错。而正常的expression能匹配到其中正常的模式,使得这段有问题的代码,也能正常工作。这就造成了我当时百思不得其解的困境:我怀疑模式匹配写得有问题,可是他可以正常工作;当我试图修改这个代码,解决expression problem问题,无论怎么修改,模式匹配都是有问题的,且遇到非常复杂的类型报错。不可谓不坑。
看这个作者的其他文章,应该对PL有所研究的人,可写出来的OCaml代码,模式匹配错误得一塌糊涂。同时,由于我对这个领域不熟悉,这算是初次有动手的尝试,之前只是看看别人的文章。万事开头难。
错误的文章
Anders Janmy 的《Solving the Expression Problem in Javascript》,试图用JavaScript解决expression problem,而JS的类型(dynamic style)显然不足以实现一个类型安全的代码。得益于JS的语言可以随意给对象或构造函数添加protype,JS实现expression,并具有拓展性,是很容易的事情。但这个显然意义不大,我们需要的是类型安全的实现。
不过,这倒是可以看出JS不足以及优点。姑且记录一下其实现。
Now lets solve it with Javascript in a dynamic style. The solution we have looks a lot like the subtype polymorphic solution above.
function Add(e1, e2) {
this.e1 = e1;
this.e2 = e2;
}
Add.prototype.value = function() { return this.e1.value() + this.e2.value(); };
function Sub(e1, e2) {
this.e1 = e1;
this.e2 = e2;
}
Sub.prototype.value = function() { return this.e1.value() - this.e2.value(); };
function Num(n) {
this.n = n;
}
Num.prototype.value = function() { return this.n; };
But, what about adding a new functions? It turns out that this is just as easy because of the dynamic nature of Javascript. We just add them to the prototype.
// Adding new functions to existing prototypes
Add.prototype.toString = function() {
return '(' + this.e1.toString() + ' + ' + this.e2.toString() + ')';
}
Sub.prototype.toString = function() {
return '(' + this.e1.toString() + ' - ' + this.e2.toString() + ')';
}
Num.prototype.toString = function() {
return '' + this.n;
}
Mul.prototype.toString = function() {
return '(' + this.e1.toString() + ' * ' + this.e2.toString() + ')';
}
Now getting a string representation of an expression is a simple as:
var x = new Num(1);
var y = new Num(2);
var z = new Add(x, y);
var w = new Sub(x, y);
var e = new Mul(z, w);
e.toString(); // returns ((1 + 2) * (1 - 2))
概念的本质
我觉得这个问题与subtyping,有深刻的联系,而subtyping我目前不能深入研究,暂且记录在这里,以后补上。估计要到读完《The Little Typer》以后。
完整可运行代码
code of SICP and Expression Problem
上篇
change log
-
2019/11/21 created document
-
2019/11/21 晚上11点完成文章结构整理