幺半群与计算机编程

计算 Fibonacci numbers

定义

依据定义实现


int fib0(int n) {
  if (n == 0) {
    return 0;
  }
  if (n == 1) {
    return 1;
  }
  return fib0(n - 1) + fib0(n - 2);
}

这个实现做了很多重复运算。例如fib0(5):


F5 = F4 + F3
   = (F3 + F2) + (F2 + F1)
   = ((F2 + F1) + (F1 + F0)) + ((F1 + F0) + F1)
   = (((F1 + F0) + F1) + (F1 + F0))+ ((F1 + F0) + F1)

我们看到(F1 + F0)被重复计算了3次。用T(n)标识fib0所需要的基本操作次数。如果n < 2，程序很快结束，仅仅执行很少的操作，从而有：

` 当n <= 1 时，T(n) <= 2`

当n增大，fib0被递归调用2次，还有3次基本操作，故：

等 n >= 1 时，T(n) = T(n-1) + T(n-2) + 3

我们将此与Fn的递推关系比较，可知T(n) >= Fn。即算法的复杂度和Fibonacci数的增长速度一样。而Fibonacci数的与2的幂增长速度相当，大概是Fn = 2 ^ (0.694n)

带缓存的实现

#include <utility>

int fib1(int n) {
  if (n == 0) {
    return 0;
  }
  std::pair<int, int> v = {0, 1};
  for (int i = 1; i < n; ++i) {
    v = {v.second, v.firt + v.second};
  }
  return v.second;
}

这个算法的复杂度是O(n)。fib1的复杂度是关于n的线性的，从指数降至多项式n。

大数的情况

在fib0和fib1中，我们都将+操作视为基本操作，认为消耗的时间是常量。而实际上大数的算术操作不能在常量的时间内完成。在大数的情况，我们需要对算法的复杂度重新计算。两个n为的二进制数的加法复杂度正比于n。

那么在fib1算法中，大概进行了Fn次加法操作，即fib2的在大数情况下的复杂度为n^2。仍然是n的多项式，依然比fib0的指数级算法优越。

求Fibonacci数通项

线性代数办法。

注：生成函数求Fibonacci数通项见《具体数学》。

用矩阵来求Fibonacci数

我们用矩阵来表示求Fibonacci数的操作：

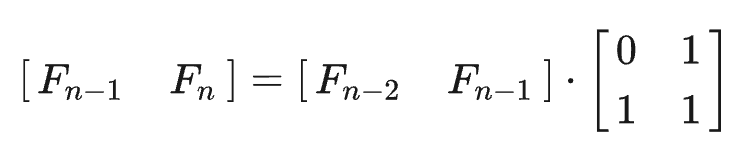
Fibonacci

设：

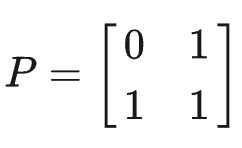
Fibonacci

则：

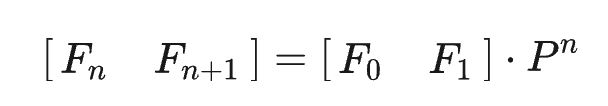
Fibonacci

记此算法为fib2。

即计算Fn只需要计算矩阵A的自乘。计算A^n最少需要多少次矩阵乘法呢？见下文的求矩阵n次幂。

我们来用矩阵求解一下通项：

  1. 求矩阵P的特征值

(A - λI)x = 0

  1. 这个线性方程有解，则(A - λI)行列式为0：det(A - λI)=0，即：λ^2 - λ - 1 = 0

求出λ，代入(A - λI)x = 0，即可求得特性向量。化简A为对角阵Λ，利用对角阵求矩阵幂，即可求得：

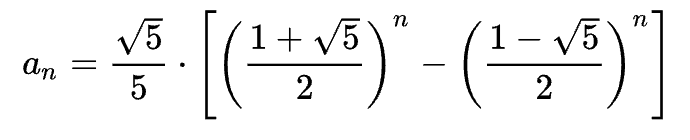
Fibonacci

当n趋近无穷大时，第二项由于小于1，剩余第一项，此时F(n+1)比F(n)为:

(1+5^2)/2

即黄金分割Ф。

反过来想，Fibonacci数列是一个整数数列，其通项居然是用无理数的幂来表示的。我们如果求得了Fibonacci数，利用这个关系，就可以求得无理数的幂。

半群

求矩阵的n次幂

矩阵的快速幂算法：


bool odd(int n) { return n & 0x1; }
int half(int n) { return n >> 1; }

template <Matrix A,  Integer N, MatrixMultiply Op>
A power_matrix(A a, N n, Op op) {

  while(!odd(n)) {
    a = op(a, a);
    n = half(n);
  }

  if (n == 1) {
    return a;
  }
  return power_accumulate_matrix(a, op(a, a), half(n - 1), op);
}

// 计算 r * (a^n)
// 乘积累加函数
// r为运算中持续更新的值
// n和a为乘数
// Op为矩阵乘法操作，此处暂未实现
template <Matrix A,  Integer N, MatrixMultiply Op>
A power_accumulate_matrix(A r, A a, N n, Op op) {
  // precondition(n >= 0);
  if (n == 0) {
    return r;
  }
  while(true) {
    if (odd(n)) {
      r = op(r, a);
      if (n == 1) {
        return r;
      }
    }
    n = half(n);
    a = op(a, a);
  }
}

从以上算法，我们知道矩阵的n次方，只需O(logn)次乘法(实际上应该还可以进一步降低，考虑乘法琏)。用矩阵的算法只需O(logn)次，而fib1需要O(n)次，我们的算法又得到新的提升。

埃及乘法(Egyptian multiplication)或俄罗斯农夫算法(Russian Peasant Algorithm)

乘法可以看做“某个数多次加到其自身”。即乘法可以用加法来计算。

1 * a = a

(n + 1) * a = n * a + a

对应的算法：


int multiply0(int n, int a) {
  if (n == 2) {
    return a;
  }
  return multiply0(n - 1, a) + a;
}

我们考察：

4a = ((a + a) + a) + a
   = (a + a) + (a + a)

依赖加法的结合律：a + (b + c) = (a + b) + c

这样我们只需计算a + a一次即可，降低了加法的运算次数。我们优化multiply0算法，可以得到：


bool odd(int n) { return n & 0x1; }
int half(int n) { return n >> 1; }

int multiply_int(int n, int a) {
  while(!odd(n)) {
    a = a + a;
    n = half(n);
  }
  if (n == 1) {
    return a;
  }
  return mult_acc_int(a, half(n - 1), a + a);
}

// 乘积累加函数
// r为运算中持续更新的值
// n和a为乘数
int mult_acc_int(int r, int n, int a) {
  while(true) {
    if (odd(n)) {
      r = r + a;
      if (n == 1) {
        return r;
      }
    }
    n = half(n);
    a = a + a;
  }
}

抽象

我们对比power_matrix和multiply_int，发现二者除了类型不一致，其他算法本身是一样的。我们把power_matrix抽象一下：

bool odd(int n) { return n & 0x1; }
int half(int n) { return n >> 1; }

template <Regular A,  Integer N, SemigroupOperation Op>
// requires (Domain<Op, A>) OP运算的定义域必须是A。C++支持concept，则可以转换为类似断言的语句(assertion)，从编译阶段保证类型直接的相互关系
A power_semigroup(A a, N n, Op op) {
  // precondition(n > 0);
  while(!odd(n)) {
    a = op(a, a);
    n = half(n);
  }

  if (n == 1) {
    return a;
  }
  return power_accumulate_semigroup(a, op(a, a), half(n - 1), op);
}

// 计算 r * (a^n)
// 乘积累加函数
// r为运算中持续更新的值
// n和a为乘数
template <Reguler A,  Integer N, SemigroupOperation Op>
// requires (Domain<Op, A>)
A power_accumulate_semigroup(A r, A a, N n, Op op) {
  // precondition(n >= 0);
  if (n == 0) {
    return r;
  }
  while(true) {
    if (odd(n)) {
      r = op(r, a);
      if (n == 1) {
        return r;
      }
    }
    n = half(n);
    a = op(a, a);
  }
}

我们考虑类型A所满足的要求。

定义常规类型T(regular type)：像int等内置类型一样，支持同类数据之间进行构造、赋值和等价测试的类型。

那么A的要求为：

幺半群(monoid)

半群(semigroup)定义：支持二元运算且运算具有结合性的代数结构。

即：

举例：正整数构成的加法半群，元素是正整数，运算是加法。

幺半群(monid)定义：支持二元运算，具有结合性，且具有单位元的代数结构。

相对半群，增加了单位元的要求。即：

举例：整数构成的乘法幺半群：元素是整数，运算是乘法，单位元是1。

我们可以把power_semigroup算拓展一下，支持单位元。由于不知道op参数代表的运算，我们需要通过op参数来确定单位元。

template <Reguler A,  Integer N, MonoidOperation Op>
// requires (Domain<Op, A>)
A power_monoid(A r, A a, N n, Op op) {
  // precondition(n >= 0);
  if (n == 0) {
    return indentity_element(op);
  }
  return power_semigroup(a, n, op);
}

// + 和 * 的indentity_element 函数
template <NoncommutativeAdditiveMonoid T>
T indentity_element(std::plus<T>) { return T(0);};

template <MultiplicativeMonoid T>
T indentity_element(std::multiplies<T>) { return T(1);};

A支持二元运算，支持结合性公理(支持等价判断，且满足结合性)。

我们考察埃及乘法(Egyptian multiplication)和矩阵乘法。二者的对象和运算，整数和加法，矩阵和矩阵乘法，二者构成了乘法幺半群，故二者可以用相同的算法实现。因此，适用于乘法幺半群的power算法，可用用于求解斐波那契数列的矩阵乘法，其复杂度为log(n)。

大数情况下Fibonacci numbers算法分析

我们分析一下，矩阵的算法性能提升的原因在于，算法中不只有加法，还有乘法。大数的乘法要慢于加法。考虑大数操作，fib1的复杂度变为O(n^2)。

假设两个n二进制数相乘的运行时间是M(n)，在没有优化的情况下，M(n)=O(n^2)。那么fib2的复杂度为O(M(n)logn)，M(n)的增长大于logn，故fib2的复杂度为O(M(n))。即fib2的算法能否比fib1快，取决于我们能否以少于O(n^2)的次数来完成两个n位数相乘。

实际上我们有处理大数相乘的算法，复杂度为O(nlogn)。我们考虑FFT算法，虽然FFT针对的是多项式相乘，我们可以把多项式的x替换为基数2，并留意进位值，这样多项式相乘就变为了普通乘法。而实际上多项式乘法构成半群，而整数乘法也是半群（考虑单位元1，即为幺半群），二者有代数结构同构。所以，针对多项式的算法，同样可以用在整数相乘上。

半群与补码

补码(two’s-complement)

将字的最有效位解释为负权(negative weight)，我们用函数B2T(Binary to Two’s-complement的缩写，长度为w)来表示。假设一个整数数据类型有w位。我们可以用向量来表示位，向量x表示[x_w-1, ..., x_1, x_0]，表示向量中的每一位，长度为w。

b2t

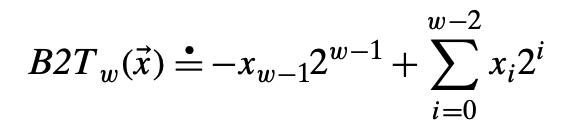
其中≐表示左边被定义为右边。B2T将一个长度为w的0、1串映射为负整数。最小值的位向量是[1, 0, ..., 0]，即最高位为负权1，但其他所有位为0，最小值TMin为-2^(w-1)。最大值TMax用位向量[0, 1, ..., 1]表示，即最大值为2^(w-1) - 1。由定义可知，每一个介于0 ~ 2^w - 1之间的数，都有唯一的w位编码。反过来，每一个w长度的位向量，都有一个唯一的值与之对应。用数学语言来说，B2T是一个双射。

最高有效位w-1位为符号位，权重为-2^(w-1)。符号位为1，为负数，0位正数。我们举例来看B2T从位向量到整数的映射：

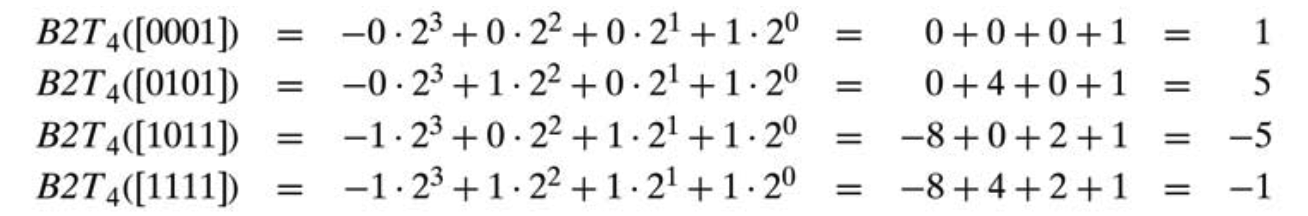
b2t_eg

无符号数的编码

把向量x看作一个二进制表示的数，我们就得到了x的无符号表示，我们用函数B2U(Binary to Unsigned)来表示，长度为w：

b2u

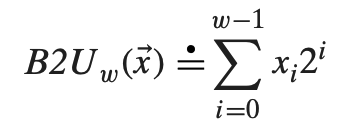
其中≐表示左边被定义为右边。B2U将一个长度为w的0、1串映射为非负整数。最大值UMax用位向量[1, 1, ..., 1]表示，即最大值为2^w - 1。由定义可知，每一个介于0 ~ 2^w - 1之间的数，都有唯一的w位编码。反过来，每一个w长度的位向量，都有一个唯一的值与之对应。用数学语言来说，B2U也是一个双射。

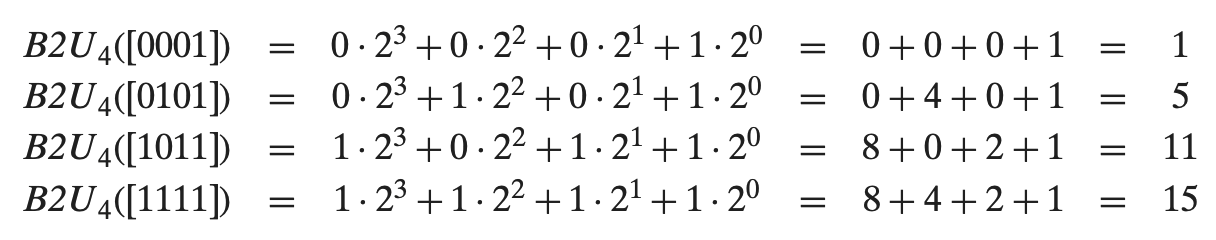
b2u_eg

分析对比补码和无符号数的编码

第一，从最大值和最小值来看，补码的最大值和最小值是不对称的，负数比非负数多一个。因为一半位模式标识负数，一半标识非负数，而0是非负数，故正数比负数少一个。

第二，最大的无符号数正好比补码的最大值的两倍大1，UMax=2TMax + 1。

从数学角度看，无符号整数的加法，构成幺半群。从补码的定义来看，除去最高位表示负权，其他和无符号整数一样，也构成幺半群。二者的加法都是二元运算，无符号整数的幺半群和补码的幺半群是否类似的呢？

我们知道无符号整数A的补码，为对A取反，再加1。取反在二进制中等价于UMax2^w-1减去A。即反码B为2^w - 1 - A，补码为2^w - 1 - A + 1，即2^w - A。

同构(isomorphic)

在抽象代数中，同构的群具有相同的性质，不需要加以区分。

同构(isomorphic)的定义:如果两个模型的元素之间有一一对应的映射关系，使得无论是先执行前者所定义的运算，然后再将其映射到后者，还是先对前者做映射，然后再执行后者所定义的运算，都能得到相同的结果，那么，这两个模型就是同构。

模型(model)定义：对于集合中的元素，如果涉及这些元素的所有运算都在理论系统中有定义，且涉及这些元素的所有命题都成立，那该集合就称为这套理论系统的模型。

其中g表示映射，f表示运算。

          g
    x,y -----> a,b
     |          |
   f |          | f
     ↓          ↓
  f(x,y) --> f(a, b) = g(x, y)
          g

举例：自然数加法模型与偶自然数加法模型之间，有乘以2的映射关系。如果两个自然数先运算(相加)，再做映射(乘以2)。那么其结果，与先做映射，再进行运算是一样的。

       乘2
   3,4 ---> 6,8
相加 ↓        ↓  相加
    7 ----> 14
      乘2

我们来看补码与无符号正整数之间的关系。g表示求补码，f表示相加

          g
    x,y -----> 2^w - 1 - x + 1, 2^w - 1 - y + 1
     |          |
   f |          | f
     ↓          ↓
    x+y --> 2^w - (x + y)  ≡ 2 * 2^w - (x + y) (mod (2^(w-1)))
          g

最后一步同余运算，在补码中是很自然处理的。补码从工程角度看，就是为了把减法转化为加法，这样在硬件层面，就可以省去加法的硬件实现。而补码的之所以能把减法转化为加法，是因为在定长的二进制位上，可以减法可以表示为求模之后的加法。我们可以看到，无论是先求补码，再相加，还是先相加再求补码，结果是一样的。故补码的加法幺半群和普通的无符号正整数的加法幺半群同构。也就是是我们可以在补码上，可以随意执行和无符号正整数一样的加法，无需做额外的处理。

当前计算机对负数主要产用补码表示。我们还有两种负数的表示：

使用原码来运算，需要判断最高位符合，做减法还需要判断两个数的大小，然后判断两个数绝对值大小，大的减小的。反码把减法转化为加法了，但反码中有两个0，+0: 0000和-0: 1111，二者都表示0。虽然从技术角度看，这不过是浪费了一个码点，但从数学的角度看，我们在一个二元运算中，有两个单位元，从而破坏了群结构，无法构成一个加法幺半群。

STL之父Alex Stepannov

问：STL一开始被设想成今天这个样子吗?即所谓的C++标准库，或者，别的什么项目发展变化而来的？告诉我们一些关于STL的历史好吗?

Alex：1976年，又要说到原苏联了。我因为吃生鱼片严重食物中毒而住院，在精神恍惚中，我忽然意识到并发的加法计算能力是基于加法是结合性的[译注：比如说a+b+c+d=(a+b) +(c+d) ] 。因此，STL可以说是细菌传染的结果。同时，我意识到并发的减法运算是和半群结构类型有关联的，这就是最基本的重点：算法是定义于代数结构基础之上的。我又花了一些年头，意识到必须在正规公理上加入复杂性必要条件以扩展结构的概念，接着又花了15年之久才完成全面的架构(我直到现在都不能确定我是否成功地让我朋友小圈子之外的任何人理解了这一点)。我相信迭代器理论是计算科学的中心，就像环或Banach区间理论是数学的中心一样。每次当我找到一个算法时，我都要努力去寻求它所定义的结构基础。我想做的就是泛化地描述算法，并乐此不疲。我可以花一个月时间去精确地描述一个众所周知的算法的泛化表示。迄今为止，在向人们解释我这种行为的重要性方面，我是异乎寻常的失败。然而，不知何故，这种行为的结果一STL却是如此成功。

问：您对面向对象是怎样理解的?它是不是一种好的可接受的编程思考方式? 有没有学习OO必须的有用的工具?

Alex：我尽量避免用OO思考问题，我对他们编程的方法不感冒。在意大利的一 家期刊采访我时我曾说过：“我发现OOP 在技术上是有问题的，它妄图用基于单一类型的不同接口来分解世界，为了处理不同的实际问题，你需要不同种类的代数方法以横跨不同类型的接口族； 我发现OOP在思想上是不健全的，它声称一切都是一个对象。即使真的是这样，也没什么意思说一切都是对象跟什么都没说一样；我发现OOP的方法论是错误的。它从类开始，就好像数学要从公理开始一样。你不是从公理开始—— 你是从证明开始的。直到你找到了一大堆相关证据你才能归纳出公理，以公理结束。编程上存在着同样的事实：你要从有趣的算法开始。只有很好地理解了算法，你才有可能提出合理的接口让其他组件共同工作。”我再重复强调一点：程序是描述算法和数据结构的，而不是描述继承性和多态性的。

问：您认为编程的好方法是什么?对于编程来说，一种工具是不是必需的?

Alex：我认为学习多种不同的编程语言是非常重要的。我用过Algol-60， Common Lisp，Scheme，Ada，C，C++，Java，和多种汇编语言。然而，也不能仅仅局限于程序语言，它仅仅是种表达算法和数据结构的工具—一 并且是种有缺陷的工具。如Niklaus Wirth有句精辟的见解：程序=算法+数据结构。

问：您认为计算机语言和人类的语言有什么区别?

Alex：没有人尝试过用计算机语言写出诗歌来。计算机语言发展到能允许我们解决一些真正美好的现实生活中的东西，还有很长的路要走。

参考资料

change log